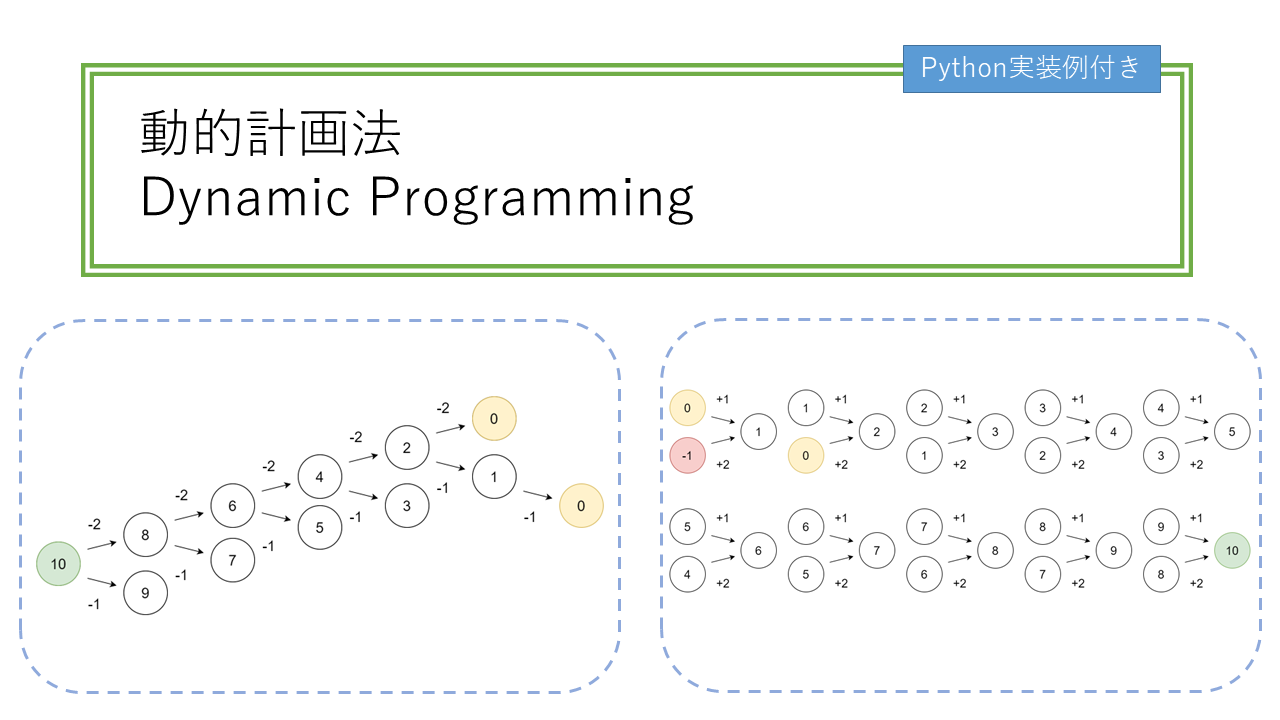
【Pythonアルゴリズム】動的計画法（Dynamic Programming）

Python

こちらは「動的計画法：Dynamic Programming」についての記事となっております。
また、Pythonによる実装例に関しても記載しております。

動的計画法 (Bottom to Top)

### Algorithim

### init dp list 
dp[0]  = 1
dp[1]  = -1
dp[2]  = -1
dp[3]  = -1
dp[4]  = -1
dp[5]  = -1
dp[6]  = -1
dp[7]  = -1
dp[8]  = -1
dp[9]  = -1
dp[10] = -1
dp[-1] = 0
dp[-2] = 0

### update process

root1: step +1
root2: step +2
dp[i] = root1 + root2 

### update dp list

# case: i = 1 

root1 = dp[0]  = 1 ### step +1
root2 = dp[-1] = 0 ### step +2
dp[1] = root1 + root2 = 1

# case: i = 2

root1 = dp[1]  = 1 ### step +1
root2 = dp[0]  = 1 ### step +2
dp[1] = root1 + root2 = 2

...

# case: i = 10

root1 = dp[9]  = 55 ### step +1
root2 = dp[8]  = 34 ### step +2
dp[10] = root1 + root2 = 89
### Python Code

### DP Bottom to Top
def dpFunc(n):
    """
    :type n: int
    :rtype: int
    """
    dp = [-1] * (n + 1)
    dp[0] = 1
    
    for i in range(1, n + 1):
        root_1 = dp[i - 1] if i - 1 >= 0 else 0
        root_2 = dp[i - 2] if i - 2 >= 0 else 0
        dp[i] = root_1 + root_2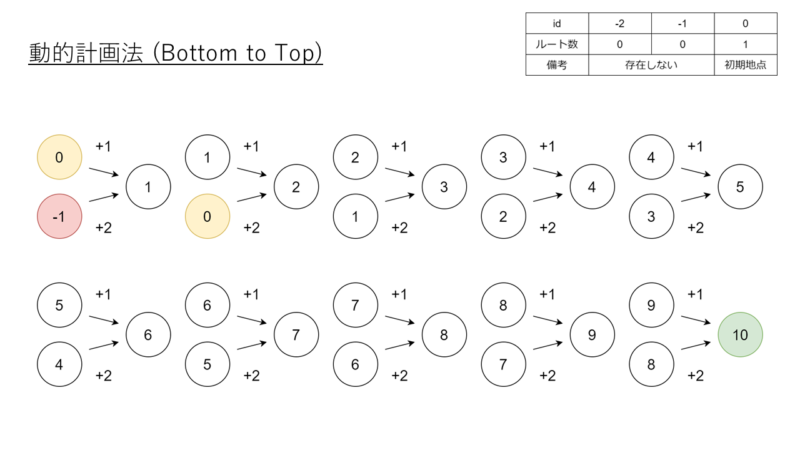

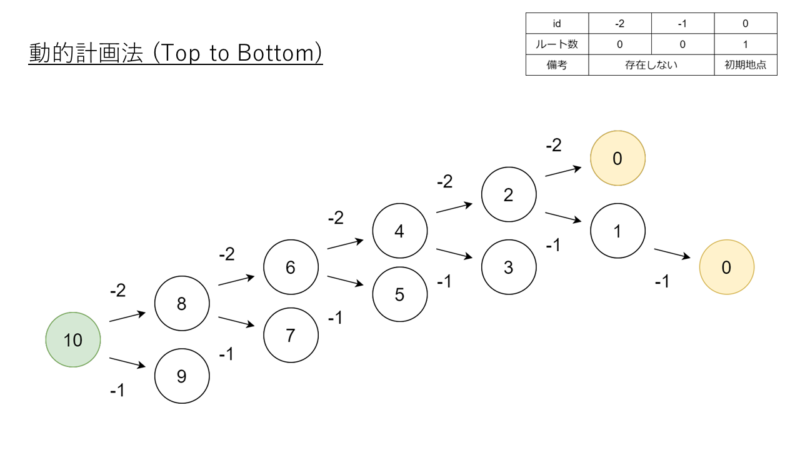
動的計画法 (Top to Bottom)

### Algorithim

### init dp list 
dp[0]  = 1
dp[1]  = -1
dp[2]  = -1
dp[3]  = -1
dp[4]  = -1
dp[5]  = -1
dp[6]  = -1
dp[7]  = -1
dp[8]  = -1
dp[9]  = -1
dp[10] = -1
dp[-1] = 0
dp[-2] = 0

### update dp list

root1: step +1
root2: step +2
dp[i] = root1 + root2 

### recursive function

refFunc(num):
	if num < 0: return 0
	if dp[num]!=-1: return dp[num]
	else:
		root1 = refFunc[num-1] ### step +1
		root2 = refFunc[num-2] ### step +2
		dp[num] = root1 + root2